Numero Pi

Número Pi

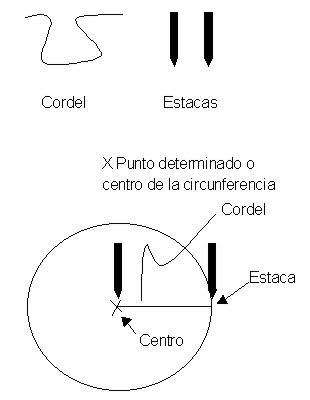
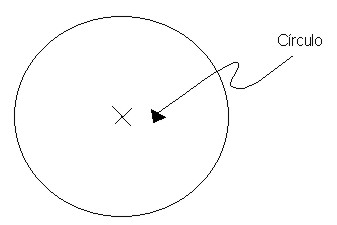
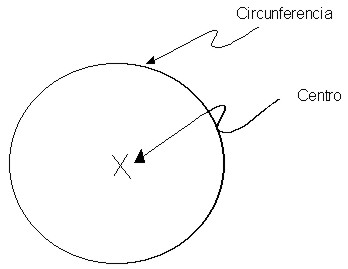
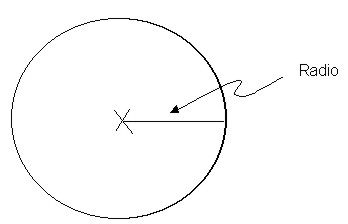
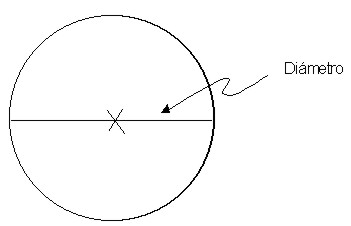
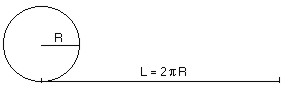
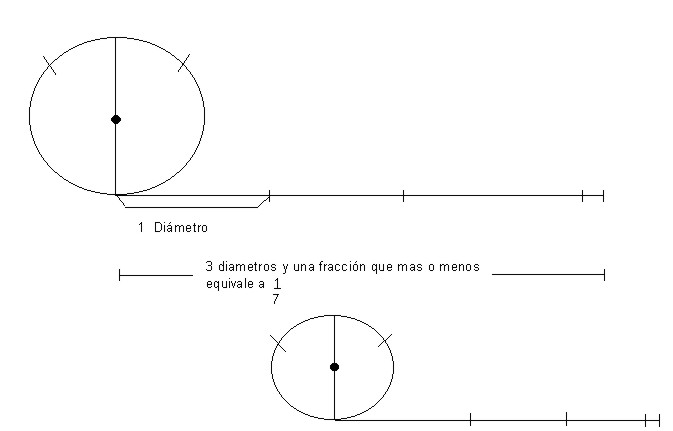
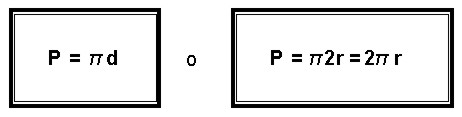
El número pi es la constante que relaciona el perímetro de una circunferencia con la amplitud de su diámetro: Π = L/D.

Este no es un número exacto sino que es de los llamados irracionales, ya que tiene infinitas cifras decimales.

Pi, como concepto, presente en Egipto

Ya en la antigüedad, se insinuó que todos los círculos conservaban una estrecha dependencia entre el contorno y su radio pero tan sólo desde el siglo XVII la correlación se convirtió en un dígito y fue identificado con el nombre "Pi" (deperiphereia, denominación que los griegos daban al perímetro de un círculo).

Esta notación fue usada por primera vez en 1706 por el matemático galés William Jones y popularizada por el matemático Leonard Euler en su obra "Introducción al cálculo infinitesimal" de 1748. Fue conocida anteriormente como constante de Ludoph(en honor al matemático Ludolph van Ceulen) o como constante de Arquímedes (No se debe confundir con el número de Arquímedes).

El valor computado de esta constante ha sido conocido con diferentes precisiones en el curso de la historia, de esta forma en una de las referencias documentadas más antiguas como la Biblia aparece de forma indirecta asociada con el número natural 3 y en Mesopotamia los matemáticos la empleaban como 3 y una fracción añadida de 1/8.

Pi (π) es una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e, y es, tal vez por ello la constante que más pasiones desata entre los matemáticos profesionales y aficionados.

Un coetáneo de Sócrates, Antiphon, inscribió en el círculo un cuadrado, luego un octógono e ideó multiplicar la cantidad de lados hasta el momento en que el polígono obtenido ajustara casi con el anillo.

Euclides

Euclides precisa en sus Elementos los pasos al límite necesarios e investiga un sistema consistente en doblar, al igual que Antiphon, el número de lados de los polígonos regulares y en demostrar la convergencia del procedimiento.

Arquímedes reúne y amplía estos resultados. Prueba que el área de un círculo es la mitad del producto de su radio por la circunferencia y que la relación del perímetro al diámetro está comprendida entre 3,14084 y 3,14285.

En el siglo II d. de C., Ptolomeo utiliza polígonos de hasta 720 lados y una circunferencia de 60 unidades de radio para  aproximarse un poco más, y da el valor 3 + 8/60 + 30/3600 = 377/120 =3'14166...

Conforme se han desarrollado las matemáticas, en sus diversas ramas, álgebra, cálculo, etc., se han ido construyendo distintos artificios que permiten afinar cada vez más su valor.

Ptolomeo

Uno de los casos más curiosos de la historia fue el del matemático inglés William Shanks, quien luego de un trabajo que le demandó casi veinte años, obtuvo 707 decimales en 1853. Desgraciadamente, Shanks incurrió en un error en el 528º decimal, y a partir de éste están todos mal.

Desde esa fecha hacia delante, se han consignado los siguientes resultados en la búsqueda de un valor para Pi:

Ferguson, en 1947, obtuvo un valor con 808 decimales. 

Usando el computador Pegasus, en 1597, se logró una cifra con 7.840 decimales. 

Más tarde, en 1961, usando un computador IBM 7090, se logró llegar a 100.000 decimales. 

Luego, en 1967, con un CDC 6600, se llegó a 500.000 decimales. 

En 1987, con un Cray-2, se obtuvo una cifra con 100.000.000 decimales para Pi..

Y finalmente, en 1995, en la Universidad de Tokio, se llegó a un valor de pi de 3,14… y se le agregan 4.294.960.000 de decimales.

Letra griega pi. Símbolo adoptado inicialmente en 1706 por William Jones y popularizado por Euler. El valor numérico de π truncado a sus diez primeras posiciones decimales, es el siguiente:

ÁREA DE CUADRILÁTEROS Y TRIÁNGULOS

Cuadriláteros
Dentro de los cuadriláteros podemos distinguir tres grupos: los paralelogramos, los trapecios y trapezoides.

1) Paralelogramos: son aquellos cuadriláteros que poseen dos pares de lados paralelos.

Cuadrados y rectángulos

Dibujaremos un cuadrado de 3 cm y colocaremos sobre él centímetros cuadrados.



Obtuvimos 9 cm2, lo mismo que si multiplicamos lado por lado, de este modo:

3 cm x 3 cm = 9 cm2

Si llamamos a al lado del cuadrado, podemos concluir que:

El área de un cuadrado es a x a = a2

El área de un rectángulo se calcula de forma semejante, lo único que cambia es que las medidas de los lados son distintas. Al largo, lo denominaremos a, y al ancho, b. Calcularemos el área del siguiente rectángulo con centímetros cuadrados.

El área equivale a 8 cm2.

Matemáticamente se puede obtener multiplicando largo por ancho.

En fórmula, el área de un rectángulo es a x b, donde a es el alto y b, la altura.

Rombos y romboides

Estos paralelogramos no tienen ángulos rectos, por lo que en ellos no se puede aplicar la misma fórmula. Para calcular su área, recurriremos a un elemento secundario: la altura, un segmento perpendicular (forma ángulos de 90°) que une un lado con su vértice opuesto.

En el rombo y romboide dibujados, DE corresponde a la altura.

¿Por qué necesitamos la altura para calcular el área?

Trazaremos una paralela a la altura desde C y prolongaremos el lado AB hasta obtener F.
Se formó un triángulo BFC, congruente con AED y nos quedó el rectángulo EFCD.



El rectángulo formado tiene como largo el lado del rombo o romboide, y su ancho es la altura dibujada. Entonces, concluimos que:

El área del rombo o romboide = b x h, donde b es la base y h, la altura

En resumen, cualquier paralelogramo tiene una sola fórmula para calcular su área, ya que, en el cuadrado y en el rectángulo, un lado es la base y el otro, la altura. Entonces:

Área de un paralelogramo = b x h, donde b es la base y h, la altura

Veamos un ejemplo:

Calculemos el área de un rombo que tiene 4,6 cm por lado y su altura es de 3 cm. Apliquemos la fórmula:

Área rombo = b x h
Área rombo = 4,6 cm x 3 cm
Área rombo = 13,8 cm2

2) Trapecios: sabemos que los trapecios son cuadriláteros que tienen un par de lados paralelos llamados bases. Sus lados, es decir, los no paralelos, no son perpendiculares a las bases, salvo el trapecio rectángulo que tiene perpendicular uno de ellos. Para el cálculo de su área también necesitamos considerar la altura.



Para formar un rectángulo trazamos la paralela a DE desde B y prolongamos DC hasta formar F.

Nos queda el  AED   CFB y nuestro rectángulo es EBFD.



El rectángulo tiene como largo la mitad de la suma de las bases del trapecio y su ancho es la altura que trazamos. El área del trapecio se puede calcular aplicando la fórmula:



Calculemos el área de nuestro trapecio:



3) Trapezoides: estos cuadriláteros no poseen lados paralelos.



Para obtener el área de un trapezoide debemos aprender primero a calcular el área de un triángulo.

Triángulos
El cálculo del área de un triángulo cualquiera, se relaciona con el área de un romboide:

Área de un romboide = base x altura

¿Cómo podemos relacionar triángulo y romboide?

Lo haremos a través del siguiente dibujo:



A nuestro ABC, le trazaremos una paralela al lado AC a partir de B, y una paralela a AB a partir de C.


Se ha formado un romboide donde el  ABC es la mitad de él.

Como el  es la mitad del romboide obtenemos que el área del  es igual a la mitad del área del romboide. Entonces:

Calculemos el área del siguiente triángulo:



Reemplazando los datos en la fórmula obtenemos:



Triángulo rectángulo:

Si el  es rectángulo, su área se puede calcular por medio de sus catetos, que son los lados perpendiculares, porque un cateto es la altura del otro.
Entonces, la fórmula para su cálculo sería:



Calculemos el área del siguiente triángulo rectángulo:



Ahora que ya sabemos como obtener el área de un triángulo, podremos calcular el área de un trapezoide:

Consideremos el siguiente trapezoide:



Partiremos dibujando un trazo entre dos vértices opuestos para así obtener dos triángulos:



El área del trapezoide será la suma del área de ambos triángulos. Como sabemos que el área de un triángulo es la mitad del producto entre la base y la altura, dibujaremos ahora la altura de ambos triángulos:



El área del trapezoide será entonces la siguiente:



Como ya sabemos calcular el área de triángulos y cuadriláteros podemos obtener el área de figuras formadas por ambos.

Para distinguir la parte que se debe calcular como resultado final se procede a achurarla, es decir, se pinta o raya imitando texturas.

Algunas veces, la parte achurada está formada por la unión de áreas de figuras, por lo tanto, hay que descomponerla, luego hacer el cálculo de cada parte, y finalmente, sumarlas para encontrar el área total.

Veamos el siguiente ejemplo:Tenemos la siguiente figura



Si te das cuenta, nuestra figura está formada por un rectángulo y un triángulo, por lo tanto, el área de ésta será la suma del área de ambas figuras.

Si AB = 8 m; BC = 3 m y la altura del triángulo es 2 m. ¿Cuál es el área de nuestra figura en cm2?

Área del rectángulo = AB x BC = 8 x 3 = 24 m2
Área del triángulo = AB x H = 8 x 2 = 16 m2

Área de nuestra figura = 24 m2 + 16 m2 = 40 m2

Ahora que ya tenemos el área de nuestra figura en m2, debemos buscar su equivalencia en cm2.
Recordemos que el cm2 es una unidad de medida más pequeña que el m2, por lo tanto, tendremos que multiplicar por potencias de 100 para obtener nuestro resultado en cm2.

Veamos la siguiente tabla:



40 x 100 = 4 000 dm2
4 000 x 100 = 400 000 cm2

El área de nuestra figura es 400 000 cm2.

Otras veces, para obtener el área achurada, debemos descomponer la figura en figuras conocidas y restar sus áreas.

Veamos un ejemplo:Tenemos la siguiente figura



Nuestra figura está formada por un rectángulo y un trapecio. Para obtener el área achurada, debemos obtener el área del rectángulo y restarle el área del trapecio.

Si: AB = 1 200 mm; BC = EF = 600 mm. ¿Cuál es el área de lo achurado en cm2?

Área rectángulo = AB x BC = 1 200 x 600 = 720 000 mm2
Área trapecio = ((CD + EF) x BC) / 2 = (( 1 200 + 600) x 600) / 2 = (1 800 x 600) / 2 = 540 000 mm2

Ahora que ya tenemos el área de ambas figuras, podremos obtener el área achurada:

Área achurada = área rectángulo - área trapecio = 720 000 mm2 - 540 000 mm2 = 180 000 mm2

Busquemos ahora la equivalencia de 180 000 mm2 en cm2. Como el cm2 es una unidad de medida más grande que el mm2, debemos dividir por una potencia de 100.

Observemos la siguiente figura:



180 000 : 100 = 1 800 cm2

El área de nuestra figura es de 18 m2.

Área del círculo

Área de un círculo

El área de un círculo se obtiene aplicando la siguiente fórmula:

Donde:


Recordemos que  es un número decimal infinito que, para efectos de cálculo, lo dejamos en3,14 ó 3.

Calculemos el área de un círculo de 8 cm de diámetro:
Recordemos que el diámetro es el doble del radio, por lo tanto, el radio es de 4 cm.



El área de nuestro círculo es de 50,24 cm2.

PERÍMETRO DE UNA CIRCUNFERENCIA...

Una de las formas más difundidas de la Naturaleza es la circular. Casi todas las formas tienden a hacerse más o menos "redondeadas".

Desde la antigüedad, el hombre se ha inquietado por conocer cuál es el perímetro de una rueda o de un platillo circular, para esto ha utilizado su ingenio; por ejemplo, ideó un procedimiento para trazar un círculo sin compás. ¿Cómo funciona este procedimiento?

En primer lugar se requiere tener un cordel y dos estacas con punta; en segundo lugar, se determina un punto a partir del cual se trazará el círculo. A dicho punto se le identificará con el nombre de centro del círculo.

El cordel debe amarrarse a ambas puntas de las estacas y una de éstas se clavará en el punto escogido como centro. La otra estaca, con el cordel bien estirado marcará, entre el centro y la punta de la estaca, el radio del círculo que trazaremos haciendo girar la estaca hasta que se dibuje claramente, en el suelo o en la superficie elegida. la circunferencia.

Llamaremos círculo a la superficie interior que se encuentra limitada por la circunferencia trazada por el cordel

.

Si éste es un círculo, entonces, ¿qué es una circunferencia?

Una circunferencia es una línea curva y cerrada, en la cual todos los puntos que la conforman se encuentran a la misma distancia de un punto llamado centro.

A partir del centro se había estirado un cordel al que se le identificó con el nombre de radio. ¿Qué es el radio?

Radio es un segmento de recta que une el centro de la circunferencia con un punto cualquiera de ella.

Si el segmento de recta llamada radio se prolonga, se tendrán dos radios o bien un diámetro, entonces, ¿qué es un diámetro?

Diámetro es la recta que, pasando por el centro de la circunferencia, une dos puntos de ella.

Elaborados los conceptos de círculo y de circunferencia pensemos en el problema de cómo saber las medidas de una rueda.

Una rueda, al dar una vuelta completa, describe una trayectoria cuya longitud es el perímetro de la circunferencia de la rueda.

Si dividimos la longitud entre el diámetro de la rueda obtenemos un valor que es independiente del tamaño de la rueda. Es decir, cualquier rueda, del tamaño que sea, al dar una vuelta completa recorre un camino de una determinada longitud. Si dividimos dicha longitud entre el diámetro de la rueda siempre obtenemos el mismo valor.

Este hecho era conocido por los babilonios y ya se encuentran noticias sobre el mismo en los papiros egipcios que se conservan en el Museo Británico.

Esta relación entre la longitud de la circunferencia y su diámetro es, posiblemente, la más popular de todas las constantes matemáticas: el número Π (pi). Dicho número, irracional, ha ocupado a generaciones de matemáticos y su atractivo perdura en nuestros días, y para fines prácticos se considera que su valor es de 3,1416.

Conocemos el valor del número Π, pero ¿cómo podríamos demostrar prácticamente que en todo círculo existe una relación constante entre el diámetro y la circunferencia.

Para hacerlo debemos operar de la siguiente manera:

Tomamos dos círculos (a y b), que son de diferente tamaño y diferente diámetro. Pero sabemos que en ambos casos el diámetro cabe tres veces y una pequeña fracción (equivalente más o menos a un séptimo) en toda la circunferencia.

Luego tomaremos dos trozos de cordel, cada uno del tamaño del diámetro de cada círculo, y con ellos podremos comprobar lo anterior al colocarlos en forma sucesiva sobre las circunferencias.

Una vez comprobado lo anterior, y sabiendo que el valor representado con la letra griega Π es de 3,1416, tenemos que:

El perímetro del círculo o bien la longitud de la circunferencia será siempre igual al producto de Π (pi) por el diámetro de la misma. O bien, será igual al producto de Π por el doble del radio.

Quedando la fórmula de la siguiente manera: